حسابات التفاضل و التكامل (الحسبان) أصبحت سهلة (الجزء الأول)

تقديم: سيلفانوس طومسون

بتاريخ: 1910  (النسخة الألكترونية من الكتاب أصدرت بتاريخ 09/10/2012

لموقع: gutenberg

ترجمة: حسين نجاح الصافي

تدقيق: ريام عيسى

تصميم الصورة: امير محمد

 

حسابات التفاضل و التكامل (الحسبان) أصبحت سهلة (الجزء الأول)

إذا أخذنا بنظر الإعتبار عدد الحمقى القادرين على القيام بعمليات حسابية كالتفاضل والتكامل (الحسبان)، فإنه من المفاجئ وجود إعتقاد أنه من الصعب لأي أحمق آخر أن يتقن نفس الحيل.

بعض حيل الحسبان سهلة للغاية. بعضها الآخر صعب جداً. الحمقى الذين يكتبون كتب الرياضيات المتقدمة (وأغلبهم حمقى أذكياء) نادراً ما يقومون بإيضاح سهولة حسابات التفاضل والتكامل، بل عكس ذلك، يبدو أنهم يرغبون بإثارة إعجابك بعبقريتهم عبر شرحها بأكثر الطرق صعوبةً.

كوني غبي بشكل ملحوظ كان عليّ أن أُنسي نفسي كل الصعوبات، والآن أرجو أن أقدم لزملائي الحمقى الأجزاء غير الصعبة، قم بإتقانها بعناية، وسيتبعها الباقي. ما يمكن لأحمق أن يفعله، يمكن لآخر أن يفعله أيضاً.

الفصل الأول

لإبعادك عن المخاوف السابقة

المخاوف التي تمنع معظم الأولاد حتى من محاولة تعلم كيفية الحسبان، يمكن القضاء عليها إلى الأبد عبر إيضاح معنى الرموز الأساسية المستخدمة في عمليات الحسبان.

هذه الرموز المرعبة هي:

1. d  و الذي يعني ” القليل من”.

و بالتالي dx  يعني القليل من x، أو du يعني القليل من u. يعتقد علماء الرياضيات الاعتياديون أن تسمية d بـ”عنصر ” أكثر تهذيباً من تسميته بـ”القليل من .” 

1. ∫ والذي يمثل الحرف اللاتيني S ولكن بشكل طويل القامة، ويمكن تسميته (إن كنت ترغب بذلك) ” مجموع ” (Sum of).

بالتالي dx  تعني مجموع كل القطع الصغيرة من x، أو dt تعني مجموع كل القطع الصغيرة من t . يسمي علماء الرياضيات الاعتياديون هذا الرمز بالتكامل، الآن أصبح بإمكان أي أحمق أن يرى أنه إذا كان x مكون من الكثير من القطع الصغيرة، حيث كل واحدة منها تدعى dx، فيمكن أن تحصل على x  بجمعهم معاً.

ببساطة كلمة “تكامل” تعني ” الشيء بأكمله” إذا فكرت بمدة الوقت التي تتضمنه ساعة واحدة، يمكنك، إن أردت، أن تفكر بها على أنها مجموع 3600 قطعة صغيرة تسمى بالثواني. القطع الصغيرة الـ3600 بأكملهن مجموعات معاً يصنعن ساعة واحدة. 

من اللآن فصاعداً عندما ترى أي عبارة في الرياضيات تبدأ بهذا الرمز المرعب ∫، فيجب عليك معرفة أنه قد تم وضع هذا الرمز لكي تعلم أنك على وشك القيام بعملية جمع كل القطع الصغيرة المدلول عليها بواسطة الرموز التي تليه . هذا كل ما في الأمر.

 

الفصل الثاني

درجات الصغر المختلفة

خلال العمليات الحسابية في التفاضل و التكامل (الحسبان) سنكتشف أنه يجب التعامل مع كميات صغيرة مختلفة بدرجة صغرها.

سنتعلم أيضاً تحت أي ظروفٍ يمكننا إعتبار كمية صغيرة أنها صغيرة للغاية لدرجة أن بالإمكان تجاهلها. كل شيء يعتمد على نسبة الصغر.

قبل وضع أي قواعد لنفكر بحالات مشابهة. هنالك 60 دقيقة في الساعة الواحدة، 24 ساعة في اليوم، 7 أيام في الأسبوع. بالتالي هنالك 1440 دقيقة في اليوم الواحد و10080 دقيقة في الأسبوع الواحد.

من الواضح أن دقيقة واحدة تعتبر كمية صغيرة للغاية من الوقت مقارنة بأسبوع كامل. في الواقع، أجدادنا إعتبروها صغيرة مقارنة بساعة واحدة، وسموها “دقيقة واحدة”، للدلالة على كسر دقيق يمثل جزءاً واحداً من 60 جزء يشكلون ساعة واحدة. عندما وجدوا أنهم بحاجة إلى تقسيمات فرعية أصغر من الوقت، قاموا بتقسيم كل دقيقة إلى 60 جزء صغير، الذي تم تسميته في ذكرى ميلاد الملكة أليزابيث بـ” الدقيقة الثانية” ( بمعنى آخر، كميات صغيرة من الدرجة الثانية من الصغر). في الوقت الحاضر نسمي هذه الكميات الصغيرة من الدرجة الثانية من الصغر بـ”الثواني.” لكن القليل من الناس يعلمون سبب تسميتها بهذا الإسم.

إذا كانت دقيقة واحدة تعتبر صغيرة جداً مقارنةً بيوم واحد، فكم ستكون الثانية الواحدة صغيرة في نفس المقارنة!

مرة أخرى، فكر بالفارذنغ (قطعة نقد بريطانية) مقارنة بالسفرن (جنيه بريطاني ذهبي): بالكاد يساوي قيمة 11000  جزء. مهما كان ثمن الفارذنغ قليلاً أو كثيراً فإنه مقارنةً بالسفرن يعتبر أقل أهمية: فمن المؤكد أنه يمكن إعتباره كمية صغيرة. لكن قارن الفارذنغ بـ1000£ (جنيه إسترليني) : الفارذنغ بالنسبة لهذا المجموع الكبير لا يمثل أهمية أكبر من أهميته بالنسبة للسفرن. حتى السفرن الذهبي نسبياً يعتبر كمية ضئيلة في ثروة مليونير.

إذا حددنا أي كسر رقمي بإعتباره يشكل النسبة التي نسميها لأي غرض صغيرة نسبيًا، فإن بإستطاعتنا وبسهولة أن نحدد كسور أخرى ذات درجة أعلى من الصغر. وهكذا، لغرض الوقت، إذا كان 160 يسمى كسراً صغيراً، حينها 160 من 160 ( تعتبر كسراً صغيراً من كسر صغير) يمكن إعتباره كمية صغيرة من الدرجة الثانية من الصغر.*

أو، لأي غرض كان إذا حددنا نسبة واحد بالمئة (1100) ككسر صغير، عندها واحد بالمئة من واحد بالمئة (110,000) سيكون كسراً صغيراً من الدرجة الثانية من الصغر، و (11,000,000) سيكون كسراً صغيراً من الدرجة الثالثة من الصغر بكونه واحد بالمئة من واحد بالمئة من واحد بالمئة.

أخيراً، لنفترض أنه لغرض دقيق للغاية يتوجب علينا إعتبار (11,000,000) “صغير”. بالتالي ميقاتية (كرونومتر) من الدرجة الأولى لن تخسر أو تكتسب أكثر من نصف دقيقة في السنة الواحدة، يجب أن تحافظ على الوقت بدقة جزء في 1,051,200. لمثل هذا الغرض إذا إعتبرنا أن 11,000,000 ( واحد من مليون ) كمية صغيرة , عندها 11,000,000  من 11,000,000 ، ستساوي 11,000,000,000,000 (واحد من مليار) ستكون كمية صغيرة من الدرجة الثانية من الصغر، ويمكن تجاهلها تماماً، عن طريق المقارنة.

عندئذٍ نرى أن كلما كانت الكمية الصغيرة أصغر، كلما كان من الممكن تجاهل الكمية الصغيرة من الدرجة الثانية. بالتالي نحن نعلم أن في كل الحالات لدينا ما يبرر تجاهل الكميات الصغيرة من الدرجة الثانية أو الثالثة ( أو درجات أعلى)، إذا كانت الكمية من الدرجة الأولى صغيرة بما يكفي.

لكن يجب أن تتذكر دائماً، أن الكميات الصغيرة إذا وجدت في عبارات رياضية كعوامل مضروبة في عامل آخر، فيمكن أن تصبح مهمة إذا كان العامل الآخر كبيراً. حتى الفارذنغ يمكن أن يكون مهماً إذا ضربناه بعدة مئات.

في الحسبان نكتب dx بمعنى القليل من x. هذه الأشياء مثل dx ، du و dy ، تسمى ب”التفاضلات، ” تفاضل  x  أو  u أو y ، حسب الحالة. [ أنت تقرأها بالشكل اللآتي ، دي-إكس ، أو دي-يو ، أو دي-واي .] إذا كان dx يعني القليل من x ، و نسبياً يعتبر صغيراً، عندها لا يمكن إعتبار الكميات التالية x∙dx ، أو x2dx ، أو axdx كميات قابلة للتجاهل. لكن dx×dx يمكن أن تكون كمية قابلة للتجاهل، كونها كمية صغيرة من الدرجة الثانية من الصغر.

مثال بسيط للغاية سيكون بمثابة رسم إيضاحي.

لنعتبر x كمية تنمو بمقدار صغير لتصبح  x+dx ، حيث dx هو الإزدياد الصغير الذي تم إضافته بفعل النمو. ناتج تربيع هذا سيكون x2+2x∙dx+(dx)2. الحد الثاني لا يمكن تجاهله، لأنه كمية من الدرجة الأولى؛ بينما الحد الثالث يعتبر صغيراً من الدرجة الثانية من الصغر، كونه جزء من جزء من x2 . بالتالي إذا عبرنا عن dx رقمياً، على سبيل المثال، 160 من  x، عندها الحد الثاني سيكون 260 من x2 ، بينما الحد الثالث سيكون 13600 من x2 ، من الواضح أن الحد الأخير أقل أهمية بكثير من الحد الثاني. لكن إذا ذهبنا أبعد من ذلك وإعتبرنا dx 11000 من x ، عندها سيكون الحد الثاني 21000 من x2، بينما سيكون الحد الثالث 11,000,000 من x2 .

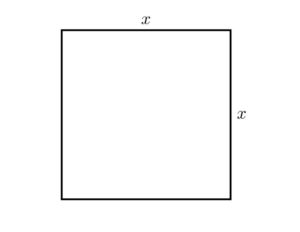
الشكل (1)

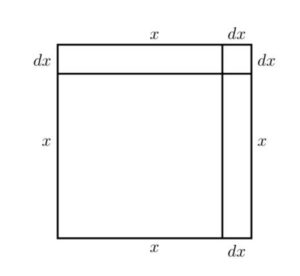
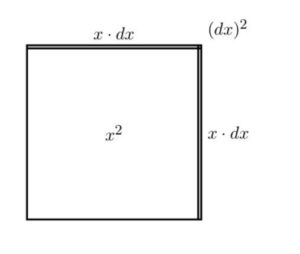
هندسياً يمكن تصوير هذا عبر رسم مربع (الشكل (1)) بطول ضلع يساوي x. الآن نعتبر أن المربع ينمو عبر إضافة القليل من dx لقياسه في كل جهة. يتكون المربع الذي تم تكبيره من المربع الأصلي x2 ، المستطيلان المتواجدان في الأعلى و على اليمين، كل منهما يشغل مساحة تساوي x⋅dx ( أو معاً 2x⋅dx)، والمربع الصغير في الزاوية اليمنى من الأعلى يشغل مساحة (dx)2. في الشكل (2) قمنا بإعتبار dx كسر كبير جداً من x، ما يقارب 15. لكن لنفترض أننا إعتبرناه 1100 ، ما يقارب سمك خط تم رسمه بقلم حبر رفيع. عندها ستكون مساحة المربع الصغير في الزاوية مساوية ل110,000 من x2 ، و ستكون غير مرئية عملياً. من الواضح أن الكمية (dx)2 تكون قابلة للتجاهل فقط إذا إعتبرنا أن الكمية dx صغيرة بما فيه الكفاية.

الشكل (2)

الشكل (3)

لنفكر بشيء مشابه.

إعتبر أن مليونير كان سيقول لأمين سره: الأسبوع القادم سأعطيك كسر صغير من أي مال سأحصل عليه. إفترض أن أمين السر كان سيقول لابنه: سأعطيك كسر صغير من ما سأحصل عليه. إعتبر أن الكسر في كل حالة هو 1100 جزء . الآن إذا كان السيد مليونير حصل خلال الأسبوع التالي على 1000£ ، أمين السر سيحصل على 10£ و الولد سيحصل على 2 شلن. عشر جنيهات قد تكون كمية صغيرة مقارنة ب1000£ ؛ لكن في الواقع 2 شلن هي كمية جد صغيرة، من الدرجة الثانية. لكن ماذا سيكون التفاوت لو أن الكسر، بدل أن يكون 1100، تم جعله 11000 جزء ؟ عندها ، بينما السيد مليونير يحصل على 1000£ ، السيد أمين السر سيحصل على 1£ فقط ، وسيحصل الولد على أقل من فارذنغ واحد! 

لقد كتب دين سويفت* البارع مرةً: 

“لذا ، يلاحظ علماء الطبيعة ، برغوث

“يملك براغيث أصغر تفترسه.

“وهذه لديها براغيث أصغر تلدغهم،

“وهكذا إلى ما لا نهاية”.

قد يكون الثور قلقاً من برغوث من الحجم الطبيعي ( كائن حي صغير من الدرجة الأولى من الصغر ). لكن على الأغلب هو لن يقلق من برغوث البرغوث؛ كونه من الدرجة الثانية من الصغر، سيكون قابل للتجاهل. حتى عدد كبير من براغيث البرغوث لن يكون بالحسبان للثور.

 

المصدر : هنا

(من الصفحة 1 إلى الصفحة 8)